저번 글에 이어서 계속한다.
1. 예제 및 복습
여기서는 책, 강의에서 제시해주는 예제를 쓰자.
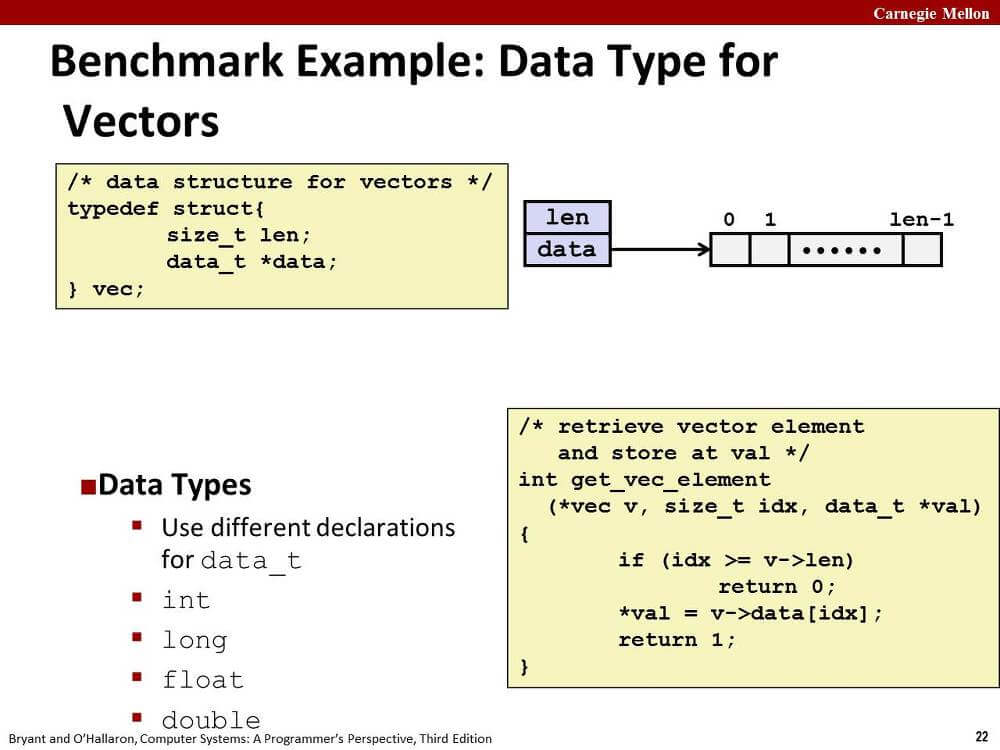
vector 자료형에 대한 연산이 정의된 combine 함수를 여러 기법을 사용해 최적화시키겠다.
가장 첫번째로 작성된 함수, combine1이다. OP는 연산자다.
void combine1(vec_ptr v, data_t *dest) {
long i;
*dest = IDENT;
for (i = 0; i < vec_length(v); i++) {
data_t val;
get_vec_element(v, i, &val);
*dest = *dest OP val;
}
}
이 코드를 CS:APP - 프로그램 최적화 1에서 정리한 대로 수정해보자.
combine4 함수.
void combine4(vec_ptr v, data_t *dest) {
long i;
long length = vec_length(v);
data_t *data = get_vec_start(v);
data_t acc = IDENT;
for (i = 0; i < length; i++) {
acc = acc OP data[i];
}
*dest = acc;
}
data_t가 double이고 OP가 *일 때 생성되는 어셈블리 코드를 비교하겠다.
아래 코드는 명령줄 옵션 -mavx2 -O1 -S를 주고 gcc를 실행한 결과다.
combine1 함수의 for문 어셈블리 코드.
.L16:
movq %r13, %rdx
movq %rbx, %rsi
movq %rbp, %rdi
call get_vec_element ; Call get_vec_element(v, i, &val)
vmovsd (%r12), %xmm0 ; Read product from dest
vmulsd 4(%rsp), %xmm0, %xmm0 ; Multiply product by data[i]
vmovsd %xmm0, (%r12) ; Store product at dest
addq $1, %rbx
cmpq 0(%rbp), %rbx
jl .L16
combine4 함수의 for문 어셈블리 코드.
.L34:
vmulsd (%rax), %xmm0, %xmm0 ; acc = acc * d[i]
addq $4, %rax ; i++
cmpq %rdx, %rax ; Compare to length:i
jne .L34
.L33:
vmovss %xmm0, (%rsi) ; Store product at dest
실제 성능 차이는 어떨까? CPE(Cycles per Element)를 측정하면 다음과 같다고 한다.
| Integer | Double FP | |||
|---|---|---|---|---|
| OP | + | * | + | * |
| Combine1 -O1 | 10.12 | 10.12 | 10.17 | 11.14 |
| Combine4 | 1.27 | 3.01 | 3.01 | 5.01 |
여기까지 어제 작성한 글 복습이다.
combine4 함수는 최적화가 끝난 것처럼 보인다. 인스트럭션 수도 최소한만 남겨둔 것 같고…
그런데 그렇지 않다. 요즘 프로세서를 고려하면 최적화 요소가 더 있다.
자세한 설명은 생략하고 기법만 정리한다. 오늘 시간이 빠듯해서;; ㅎㅎ;;
2. 루프 풀기(Loop Unrolling)
매 루프마다 계산되는 원소의 수를 증가시켜서 루프 반복실행 횟수를 줄이는 방법이다.
이 방법을 통해 얻는 이득은 두 가지다.
- 루프 인덱스 계산, 조건부 분기와 같은 연산과 직접적인 연관이 없는 연산을 줄인다.
- 전체 연산의 수를 줄이는 관점에서 최적화를 적용할 수 있다.
이 시점에서 combine4 함수의 루프문 내부를 도식화해보자. float point과 multiply 연산에 대해서 그렸다.
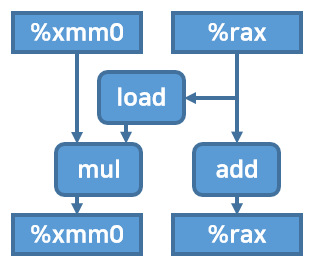
combine4 함수에 loop unrolling을 적용해보자.
한 루프에 2개의 연산을 하도록 loop unrolling을 적용하면 다음과 같은 코드와, 기계어, 그리고 도식이 나온다.
코드. 이러한 변환을 2 * 1 loop unrolling이라고 부른다.
void combine5(vec_ptr v, data_t *dest) {
long i;
long length = vec_length(v);
long limit = length - 1;
data_t *data = get_vec_start(v);
data_t acc = IDENT;
for (i = 0; i < limit; i += 2) {
acc = (acc OP data[i]) OP data[i+1];
}
for (; i < length; i++) {
acc = acc OP data[i];
}
*dest = acc;
}
기계어 (첫번째 for문)
.L39:
vmulsd (%rdx,%rax,8), %xmm0, %xmm0 ; data[i]
vmulsd 8(%rdx,%rax,8), %xmm0, %xmm0 ; data[i+1]
addq $2, %rax ; i += 2
cmpq %rax, %r8 ; Compare limit:i
jg .L39
도식
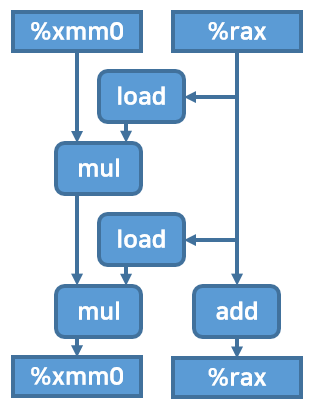
책에 의하면 CPE는 다음과 같다. 정수 덧셈 연산에 대해서는 성능이 향상됐지만 다른 연산에서는 큰 성능향상이 보이지 않는다.
| Integer | Double FP | |||
|---|---|---|---|---|
| OP | + | * | + | * |
| Combine4 | 1.27 | 3.01 | 3.01 | 5.01 |
| Combine5 | 1.01 | 3.01 | 3.01 | 5.01 |
| Latency bound | 1.00 | 3.00 | 3.00 | 3.00 |
| Throughput bound | 0.50 | 1.00 | 1.00 | 0.50 |
이제 다음 최적화를 적용해보자.
3. 재결합 변환(Reassociation Transform)
병렬성 향상을 위해 코드를 변환하는 방법이다.
위 combine5 함수 중 일부 코드를…
for (i = 0; i < limit; i += 2) {
acc = (acc OP data[i]) OP data[i+1];
}
아래와 같이 바꾸면 어떻게 될까?
for (i = 0; i < limit; i += 2) {
acc = acc OP (data[i] OP data[i+1]);
}
괄호 위치만 바뀌었는데 성능에 큰 차이가 생길까?
확인해보겠다.
어셈블리 코드는 다음과 같이 변한다.
.L66:
vmovsd (%rdx,%rax,8), %xmm1 ; %xmm1 = data[i]
vmulsd 8(%rdx,%rax,8), %xmm1, %xmm1 ; %xmm1 *= data[i+1]
vmulsd %xmm1, %xmm0, %xmm0 ; %xmm0 *= %xmm1
addq $2, %rax ; i += 2
cmpq %rax, %r8 ; Compare to limit:i
jg .L66
인스트럭션은 하나가 늘었다.
그리고 사용하는 레지스터도 하나 늘었다.
눈에 보이는 인스트럭션 차이는 중요하지 않다.
아래 도식화된 그림을 보자. %xmm1 레지스터는 그림에서 일부러 생략했다.
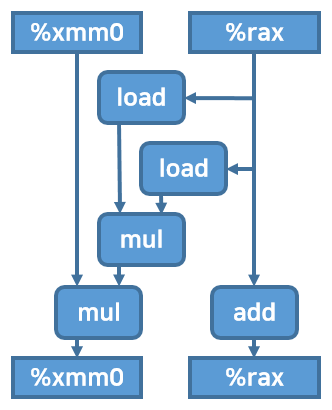
combine5 코드대로는 %xmm0에 대한 첫번째 곱연산이 끝날 때까지 두번째 곱연산을 할 수 없었다. 순차적 의존성 때문이다.
그러나 지금 코드는 %xmm0에 대한 곱연산을 하는 동안, %xmm1에 대한 곱연산을 실행할 수 있다.
그러므로 프로세서의 병렬 처리가 제대로 이루어진다면 꽤 많은 실행시간을 절약할 수 있다.
그렇다면 CPE는 어떻게 나올까? 책을 보면 아래와 같다.
| Integer | Double FP | |||
|---|---|---|---|---|
| OP | + | * | + | * |
| Combine5 | 1.01 | 3.01 | 3.01 | 5.01 |
| Combine5+ | 1.01 | 1.51 | 1.51 | 2.51 |
| Latency bound | 1.00 | 3.00 | 3.00 | 3.00 |
| Throughput bound | 0.50 | 1.00 | 1.00 | 0.50 |
거의 2배에 가까운 성능 향상을 보여준다.
4. 병렬 누산기(Separate Accumulators)
지역변수를 명시적으로 여러 개 설치해서 순차적 의존성을 깰 수도 있다.
아래 코드는 combine5 함수에 대해 누산기를 적용한 함수다.
void combine6(vec_ptr v, data_t *dest) {
long i;
long length = vec_length(v);
long limit = length - 1;
data_t *data = get_vec_start(v);
data_t acc0 = IDENT;
data_t acc1 = IDENT;
for (i = 0; i < limit; i += 2) {
acc0 = acc0 OP data[i];
acc1 = acc1 OP data[i+1];
}
for (; i < length; i++) {
acc0 = acc0 OP data[i];
}
*dest = acc0 OP acc1;
}
.L57:
vmulsd (%rdx,%rax,8), %xmm0, %xmm0 ; acc0 = acc0 * data[i];
vmulsd 8(%rdx,%rax,8), %xmm1, %xmm1 ; acc1 = acc1 * data[i+1];
addq $2, %rax
cmpq %rax, %r8
jg .L57
루프 부분의 어셈블리 코드를 보고 combine5 함수와 비교하면 두번째 인스트럭션의 두세번째 오퍼랜드가 %xmm0에서 %xmm1으로 바뀐 것을 볼 수 있다.
첫번째 vmulsd 인스트럭션과 두번째 vmulsd 인스트럭션 사이에 순차적 의존성이 없기 때문에 프로세서가 병렬로 처리할 수 있게 된다.
그림으로 보면 더 확실하다.
%xmm0에 대한 연산과 %xmm1에 대한 연산 간에 의존 관계가 없음이 한눈에 보인다.
CPE는 다음과 같다.
| Integer | Double FP | |||
|---|---|---|---|---|
| OP | + | * | + | * |
| Combine5 | 1.01 | 3.01 | 3.01 | 5.01 |
| Combine5+ | 1.01 | 1.51 | 1.51 | 2.51 |
| Combine6 | 0.81 | 1.51 | 1.51 | 2.51 |
| Latency bound | 1.00 | 3.00 | 3.00 | 3.00 |
| Throughput bound | 0.50 | 1.00 | 1.00 | 0.50 |
unrolling과 accumulating을 더 여러 개 해주면 성능이 더 좋아진다.
5. 마무리
여기서 만족하지 못하고 성능이 더 올리고 싶은 사람은 SIMD를 공부해보자.
다음에 공부할 내용은 메모리다.
출처
‘Computer Systems A Programmer’s Perspective (3rd Edition)’